applyMatrix \ Language (API)

Name

applyMatrix

Examples

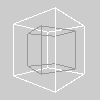
settings <- function() {
    size(100, 100, P3D)
}

draw <- function() {
    noFill()
    translate(50, 50, 0)
    rotateY(PI/6)
    stroke(153)
    box(35)
    # Set rotation angles
    ct = cos(PI/9)
    st = sin(PI/9)
    # Matrix for rotation around the Y axis
    applyMatrix(ct, 0, st, 0, 0, 1, 0, 0, -st, 0, ct, 0, 0, 0, 0, 
        1)
    stroke(255)
    box(50)
}

Description

Multiplies the current matrix by the one specified through the parameters. This is very slow because it will try to calculate the inverse of the transform, so avoid it whenever possible. The equivalent function in OpenGL is glMultMatrix().

Syntax

applyMatrix(source)
applyMatrix(n00, n01, n02, n10, n11, n12)
applyMatrix(n00, n01, n02, n03, n10, n11, n12, n13, n20, n21, n22, n23, n30, n31, n32, n33)

Parameters

n00	float: numbers which define the 4x4 matrix to be multiplied
n01	float: numbers which define the 4x4 matrix to be multiplied
n02	float: numbers which define the 4x4 matrix to be multiplied
n10	float: numbers which define the 4x4 matrix to be multiplied
n11	float: numbers which define the 4x4 matrix to be multiplied
n12	float: numbers which define the 4x4 matrix to be multiplied
n03	float: numbers which define the 4x4 matrix to be multiplied
n13	float: numbers which define the 4x4 matrix to be multiplied
n20	float: numbers which define the 4x4 matrix to be multiplied
n21	float: numbers which define the 4x4 matrix to be multiplied
n22	float: numbers which define the 4x4 matrix to be multiplied
n23	float: numbers which define the 4x4 matrix to be multiplied
n30	float: numbers which define the 4x4 matrix to be multiplied
n31	float: numbers which define the 4x4 matrix to be multiplied
n32	float: numbers which define the 4x4 matrix to be multiplied
n33	float: numbers which define the 4x4 matrix to be multiplied

pushMatrix
popMatrix
resetMatrix
printMatrix